Toolboxes for Matlab/Octave
ARESLab: Adaptive Regression Splines toolbox
Version 1.13.0 (May 15, 2016) - download (GNU GPL license)
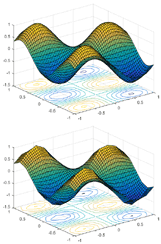
ARESLab is a Matlab/Octave toolbox for building piecewise-linear and piecewise-cubic regression models using Jerome Friedman's Multivariate Adaptive Regression Splines method (also known as MARS).
Multivariate Adaptive Regression Splines has the ability to model complex and high-dimensional data dependencies. The model takes the form of an expansion in product spline basis functions, where the number of basis functions as well as the parameters associated with each one (product degree and knot locations) are automatically determined by the data through a forward/backward iterative approach.
User's manual can be downloaded here (it is also included in the .zip file).
M5PrimeLab: M5' regression tree, model tree, and tree ensemble toolbox
Version 1.8.0 (November 6, 2020) - download (GNU GPL license)
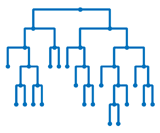
M5PrimeLab is a Matlab/Octave toolbox for building regression trees and model trees using M5' method as well as building ensembles of M5' trees using Bagging, Random Forests, and Extremely Randomized Trees. The built trees can also be linearized into decision rules either directly or using the M5'Rules method. M5PrimeLab accepts input variables to be continuous, binary, and categorical, as well as manages missing values.
Model trees combine a conventional regression tree with the possibility of linear regression functions at the leaves. This representation usually provides higher accuracy than regression trees but preserves the advantage of clear and easy-to-interpret structure.
User's manual can be downloaded here (it is also included in the .zip file).
LWP: Locally Weighted Polynomials toolbox
Version 2.2 (September 3, 2016) - download (GNU GPL license)
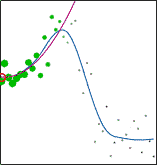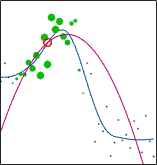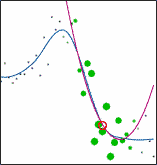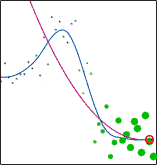
LWP is a Matlab/Octave toolbox implementing Locally Weighted Polynomial regression (also known as Local Regression / Locally Weighted Scatterplot Smoothing / LOESS / LOWESS and Kernel Smoothing). With this toolbox you can fit local polynomials of any degree using one of the nine kernels with metric window widths or nearest neighbor window widths to data of any dimensionality. A function for optimization of the kernel bandwidth is also available. The optimization can be performed using Leave-One-Out Cross-Validation, GCV, AICC, AIC, FPE, T, S, or separate validation data. Robust fitting is available as well.
Locally Weighted Polynomial regression is designed to address situations in which models of global behaviour do not perform well or cannot be effectively applied without undue effort. LWP is a nonparametric regression method that is carried out by pointwise fitting of low-degree polynomials to localized subsets of the data.
User's manual can be downloaded here (it is also included in the .zip file).
Radial Basis Function interpolation
Version 1.1 (August 12, 2009) - download (GNU GPL license)
Radial Basis Function interpolation with biharmonic, multiquadric, inverse multiquadric, thin plate spline, and Gaussian basis functions for Matlab/Octave.
RBF interpolation uses a series of basis functions that are symmetric and centered at each sampling point. Radial basis functions are a special class of functions with their main feature being that their response decreases (or increases) monotonically with distance from a central point. The center, the distance scale, and the precise shape are parameters of the model.
Patient Rule Induction Method
Version 1.0 (November 9, 2015) - download (GNU GPL license)
The toolbox implements the Patient Rule Induction Method (PRIM) for Matlab/Octave. PRIM is a method for finding 'interesting' regions (bump hunting) in high-dimensional data. The regions are described by hyper-rectangles (boxes) containing simple decision rules.
The toolbox can be used on regression-type as well as classification-type data. It accepts input variables to be continuous, binary, and categorical, as well as manages missing values.